Trick Of The Day (Alex) - Integrals and Derivates Using the Power Rule
2 posters
Page 1 of 1
 Trick Of The Day (Alex) - Integrals and Derivates Using the Power Rule
Trick Of The Day (Alex) - Integrals and Derivates Using the Power Rule
Most people you finde who are not in calculus hear the word "integral" and will generally have one of two responses; either they'll shy away from you with a pained look on their face  , or stupidly ask "What's an integral?"
, or stupidly ask "What's an integral?"
Well I'm here to teach you all I know about integrals and derivatives. Please note that I am not in Calculus yet, and I may still have some basic mistakes. Also, I cannot do very many problems.
First off, I'm going to teach the derivative.
Any variables i use will be explained by this A(X) ^ C
Example 1
Problem: 2x^6
To get the answer, you will need to multiply A * C, and subtract one from C, in that order.
So the answer would be (2*6)X^(C-1), or 12x^5.
Example 2
Problem: 3x^5 + 2x^3 + x^2
This works the same way, all you need to do is solve each term seperately.
Answer would be 15x^4 + 6X^2 + 2x.
You can make up your own problems.
Integral (extremely limited knowledge)
To take the integral of something, you basically do the reverse of the derivate. In this way, you can compare the two to subtraction and addition.
To take the integral of Ax^C, you add 1 to C and divide A by the new value of C.
Example 1
2x^1
add one to 1 -> C =2
A/C (2/2) now equals one.
So the answer, therefore, is x^2.
Example 2
x^2
Add one to ^2
divide A by three
Answer is (x^3) / 3
---
So how can this be used on Number sense tests?
Let me give you an example.
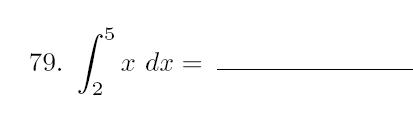
The thing you will be taking the integral of is where the x is.
For this equation, the integral of x is (x^2)/2.
You will then take the two values, and input them into the integral of said x, then subtract the lower value from the higher value.
The work(in your head, of course) would look like this
(5^2)/2 - (2^2)/2
25/2 - 4/2
21/2
The answer to this problem is 21/2.
Create some of your own examples, or use those on the past tests you have taken.
Thanks for your time, and if there are any mistakes (and I'm sure there are), feel free to post away.
Well I'm here to teach you all I know about integrals and derivatives. Please note that I am not in Calculus yet, and I may still have some basic mistakes. Also, I cannot do very many problems.
First off, I'm going to teach the derivative.
Any variables i use will be explained by this A(X) ^ C
Example 1
Problem: 2x^6
To get the answer, you will need to multiply A * C, and subtract one from C, in that order.
So the answer would be (2*6)X^(C-1), or 12x^5.
Example 2
Problem: 3x^5 + 2x^3 + x^2
This works the same way, all you need to do is solve each term seperately.
Answer would be 15x^4 + 6X^2 + 2x.
You can make up your own problems.
Integral (extremely limited knowledge)
To take the integral of something, you basically do the reverse of the derivate. In this way, you can compare the two to subtraction and addition.
To take the integral of Ax^C, you add 1 to C and divide A by the new value of C.
Example 1
2x^1
add one to 1 -> C =2
A/C (2/2) now equals one.
So the answer, therefore, is x^2.
Example 2
x^2
Add one to ^2
divide A by three
Answer is (x^3) / 3
---
So how can this be used on Number sense tests?
Let me give you an example.
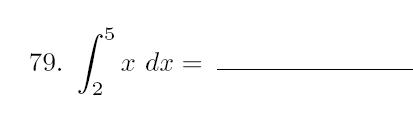
The thing you will be taking the integral of is where the x is.
For this equation, the integral of x is (x^2)/2.
You will then take the two values, and input them into the integral of said x, then subtract the lower value from the higher value.
The work(in your head, of course) would look like this
(5^2)/2 - (2^2)/2
25/2 - 4/2
21/2
The answer to this problem is 21/2.
Create some of your own examples, or use those on the past tests you have taken.
Thanks for your time, and if there are any mistakes (and I'm sure there are), feel free to post away.

Ani- Vice-President

-
 Number of posts : 236
Number of posts : 236
Age : 32
Location : Kanto
Registration date : 2008-05-02
 Similar topics
Similar topics» Trick Of The Day (Alex) - Infinite Sequences
» Trick of the Day - Multiplication by 25, 50, 75, 125
» Trick of the Day - Sum of Fibonacci
» Trick of the Day - Arithmetic Mean
» Trick of the Day - Squaring numbers between 41 and 59
» Trick of the Day - Multiplication by 25, 50, 75, 125
» Trick of the Day - Sum of Fibonacci
» Trick of the Day - Arithmetic Mean
» Trick of the Day - Squaring numbers between 41 and 59
Page 1 of 1
Permissions in this forum:
You cannot reply to topics in this forum